9. Sınıf Matematik Ders Kitabı Sayfa 83-84-85-86 Cevapları Ata Yayıncılık

2. Bölüm Ölçme ve Değerlendirme Soruları

1. Aşağıdaki ifadelerden kaç tanesi bir küme belirtir?
(Y) I. Bazı gözlüklü kız öğrenciler (Netlik yok)
(D) II. Okulumuzdaki matematik öğretmenleri
(D) III. Alfabemizdeki sesli harfler
(D) IV. Yılın M ile başlayan ayları
(D) V. Ankara’nın ilçeleri
A) 1 B) 2 C) 3 D) 4 E) 5
Cevap D) 4

2. A = {x | x ≤ 60, x = 2n, n O∈N} kümesi veriliyor.
Buna göre
B = {61’den küçük iki basamaklı çift doğal sayılar}
C = {61’den küçük çift doğal sayılar}
D = {6 ile 61 arasındaki çift doğal sayılar}
kümelerinden hangisi ya da hangileri A kümesine eşittir?
A) Yalnız B B) Yalnız C C) B ve C D) B ve D E) C ve D

B = {61’den küçük iki basamaklı çift doğal sayılar} // {10, 12, ...., 60}
C = {61’den küçük çift doğal sayılar} // {0,1,2, ..., 60}
D = {6 ile 61 arasındaki çift doğal sayılar} // {8, 10, 12, ..., 60}
Cevap) B Yalnız C

3. Aşağıdaki ifadelerde doğru olanların başına “D” yanlış olanların başına “Y” yazınız.
(D) Aynı elemanlardan oluşan kümelere eşit küme denir.
(D) A ≠ Δ, B ≠ Δ olmak üzere a O∈A ve b O∈B elemanları alınarak oluşturulan (a, b) biçimindeki yeni elemana sıralı ikili denir.
(Y) Sadece bir elemanı ortak olan kümelere ayrık kümeler denir.
(Y) A ve B gibi iki kümenin tüm elemanlarından oluşan kümeye bu kümelerin kesişim kümesi denir.

4. A = {1, 2, {1, 2}, {a}, {2} } kümesi veriliyor.
Buna göre aşağıdaki ifadelerden kaç tanesi doğrudur?
I. 1 O∈A
II. {2} O∈A
III. a O∈A
IV. 2 O∈A
V. {1, 2, {2} } ∈ A
A) 1 B) 2 C) 3 D) 4 E) 5
Cevap) C) 3
I. 1 ∊ A: Doğrudur, çünkü 1 küme A içinde bulunuyor.
II. {2} ∊ A: Doğrudur, çünkü {2} küme A içinde bulunuyor.
III. a ∊ A: Doğru değildir, çünkü "a" kendisi bir eleman değil, bir semboldür ve küme A içinde bulunmuyor.
IV. 2 ∊ A: Doğrudur, çünkü 2 küme A içinde bulunuyor.
V. {1, 2, {2}} ∊ A: Doğru değildir, çünkü {1, 2, {2}} kümesi A içinde doğrudan bulunmuyor.

5. 10 elemanlı bir kümenin alt küme sayısı kaçtır?
A) 64 B) 128 C) 256 D) 512 E) 1024
Cevap E) 1024
Bir kümenin alt kümelerinin sayısı, o küpteki eleman sayısına göre hesaplanır. Bir küpte n eleman bulunuyorsa, bu küpün alt küme sayısı 2ⁿ olur.
Verilen durumda, 10 elemanlı bir küpten alt kümelerin sayısı 2¹⁰ = 1024 olur.

6. Aşağıda verilen kümelerden kaç tanesi sonlu kümedir?
I. Ülkemizdeki tüm öğrencilerin oluşturduğu küme
II. Asal sayılar kümesi
III. Pozitif tam sayılar kümesi
IV. 5 ile 8 arasındaki gerçek sayılar kümesi
V. –50 000 ile 50 000 arasındaki tam sayılar kümesi
A) 1 B) 2 C) 3 D) 4 E) 5
Cevap B) 2
(Sayılabilir) I. Ülkemizdeki tüm öğrencilerin oluşturduğu küme
(Sonsuz) II. Asal sayılar kümesi
(Sonsuz) III. Pozitif tam sayılar kümesi
(Sonsuz) IV. 5 ile 8 arasındaki gerçek sayılar kümesi
(Sayılabilir) V. –50 000 ile 50 000 arasındaki tam sayılar kümesi

7. s(A) = 2n – 4 olmak üzere A kümesinin 256 tane alt kümesi olduğuna göre n kaçtır?
A) 4 B) 5 C) 6 D) 7 E) 8
Cevap C) 6
256 = 2⁸
2^2n-4 = 2⁸
2n - 4 = 8
2n = 12
n = 6

8. Bir kümenin alt küme sayısı ile öz alt küme sayısı toplamı aşağıdakilerden hangisi olabilir?
A) 16 B) 32 C) 64 D) 113 E) 127
Cevap D) 127

n = 4 için 2⁴ = 16 --> 16 - 1 = 15
n = 5 için 2⁵ = 32 --> 32 - 1 = 31
n = 6 için 2⁶ = 64 --> 64 - 1 = 635
n = 7 için 2⁷ = 128 --> 128 - 1 = 127

9. A = {a, b, c, d, e, f, g} kümesinin alt kümelerinden kaç tanesi a, b ve c elemanlarının
üçünü birden kapsar?
A) 16 B) 24 C) 32 D) 48 E) 64
Cevap A) 16
a,b,c elemanları yerine x yazalım
A = {x, d, e, f, g}
2⁵ = 32
32 = 2 = 16

10. A kümesinin eleman sayısı B kümesinin eleman sayısından 2 fazladır. A kümesinin alt
küme sayısı B kümesinin alt küme sayısından 768 fazla olduğuna göre A kümesinin
eleman sayısı kaçtır?
A) 8 B) 9 C) 10 D) 11 E) 12

s(A) = n + 2
s(B) = n
2ⁿ⁺² = 2ⁿ + 768
2ⁿ . 4 = 2ⁿ + 768
3 . 2ⁿ = 768
2ⁿ = 256
2ⁿ = 8
s(A) = n + 2
s(A) = 8 + 2 = 10
Cevap C) 10

11. A = {1, 2, 3, 4, 5, 6} kümesinin alt kümelerinin kaç tanesinde 1 eleman olarak bulunur 5 eleman olarak bulunmaz?
A) 2 B) 4 C) 8 D) 16 E) 32
5'i tamamen atalım
Bu durumda A kümesini tekrar yazarsak A = {1, 2, 3, 4, 6}
s(A) = 5
2⁵ = 32
32 / 2 = 16
Cevap D) 16

12. A = { a, b, c, d, e, f } kümesinin alt kümelerinin kaç tanesinde c ve f elemanlarından yalnız biri bulunur?
A) 96 B) 84 C) 64 D) 48 E) 32
Cevap E) 32
A kümesinin eleman sayısı 6'dır. Bir kümenin alt kümelerinin sayısı 2ⁿ'dir, burada n, kümenin eleman sayısıdır. Yani, A kümesinin alt kümelerinin sayısı 2⁶ = 64'tür.

c veya f elemanlarından yalnız biri bulunan alt kümelerin sayısı: Her iki elemandan yalnız birini seçmek için 2 yol vardır (c veya f). Diğer 4 elemanın alt kümede bulunmama olasılığı ise 2⁴ = 16'dır.

Toplam alt kümelerin sayısı (c veya f elemanlarından bağımsız olarak): 64

Sonuç olarak, c ve f elemanlarından yalnız birini içeren alt kümelerin sayısı: 2 x 16 = 32

Bu nedenle, A kümesinin alt kümelerinden 32 tanesinde c ve f elemanlarından yalnız biri bulunur. Doğru cevap E) 32 olacaktır.

13. E evrensel küme A ⊆ E, B ⊆ E olmak üzere aşağıdaki ifadelerden kaç tanesi doğrudur?
I. A ⊆ B ise A ∪ B = B
II. A ∪ A = E
III. B ⊆ A ise A ∩ B = B
IV. s(A) + s(Aʹ) = s(E)
V. A \ B = A ∩ Bʹ
VI. A ∪ E = E
VII. A \ E = Aʹ
VIII. E \ E = Aʹ
IX. A \ A = ∅
X. A ≠ B Ş A \ B ≠ B \ A
A) 3 B) 4 C) 5 D) 6 E) 7
Cevap E) 7
I. A ⊆ B ise A ∪ B = B: Doğru.
II. A ∪ A = E: Doğru.
III. B ⊆ A ise A ∩ B = B: Yanlış. Eğer B, A'nın alt kümesiyse, A ve B'nin kesişimi B olur.
IV. s(A) + s(Aʹ) = s(E): Doğru.
V. A \ B = A ∩ Bʹ: Doğru.
VI. A ∪ E = E: Doğru.
VII. A \ E = Aʹ: Yanlış. A'nın evrensel kümeden farkı, A'nın tümleyenine eşittir.
VIII. E \ E = Aʹ: Yanlış. Evrensel kümenin kendisinden farkı, boş kümedir.
IX. A \ A = ∅: Doğru.
X. A ≠ B Ş A \ B ≠ B \ A: Doğru.
Doğru ifadeler 7 tanedir. Doğru cevap B) 7 olacaktır.

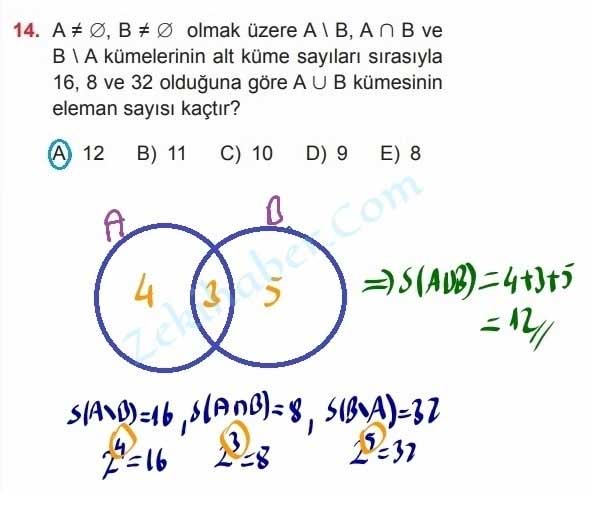
14. A ≠ Δ, B ≠ Δ olmak üzere A \ B, A ∩ B ve B \ A kümelerinin alt küme sayıları sırasıyla
16, 8 ve 32 olduğuna göre A ∪ B kümesinin eleman sayısı kaçtır?
A) 12 B) 11 C) 10 D) 9 E) 8

15. A ∪ B = {a, b, c, d, e, f, g} ve B ∪ C = {c, d, e, f, k, l, m} olduğuna göre B kümesinin en çok kaç elemanı vardır?
A) 3 B) 4 C) 5 D) 6 E) 7

16. Aşağıdaki ifadelerden kaç tanesi doğrudur?
I. ∪ işleminin değişme özelliği vardır.
II. ∩ işleminin birleşme özelliği vardır.
III. ∪ işleminin ∩ işlemi üzerine sağdan ve soldan dağılma özelliği vardır.
IV. Kümelerde fark işleminin değişme özelliği vardır.
V. Her a, b elemanları için (a, b) = (b, a) eşitliği doğrudur.
A) 1 B) 2 C) 3 D) 4 E) 5
Cevap C) 3

I. ∪ işleminin değişme özelliği vardır. (A ∪ B = B ∪ A) - Doğru.
II. ∩ işleminin birleşme özelliği vardır. (A ∩ B = B ∩ A) - Doğru.
III. ∪ işleminin ∩ işlemi üzerine sağdan ve soldan dağılma özelliği vardır. (A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)) - Doğru.
IV. Kümelerde fark işleminin değişme özelliği vardır. (A - B = B - A) - Yanlış.
V. Her a, b elemanları için (a, b) = (b, a) eşitliği doğrudur. (Bu ifade kartezyen çarpım için kullanılır ve eşittir.) - Yanlış.
Doğru ifadelerin sayısı 3'tür. Doğru cevap C) 3 olacaktır.

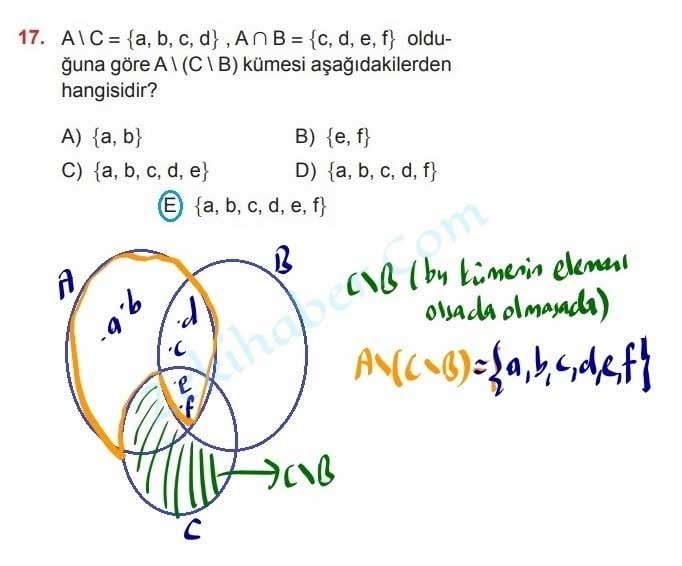
17. A \ C = {a, b, c, d} , A ∩ B = {c, d, e, f} olduğuna göre A \ (C \ B) kümesi aşağıdakilerden hangisidir?
A) {a, b} B) {e, f}
C) {a, b, c, d, e} D) {a, b, c, d, f}
E) {a, b, c, d, e, f}

18. E evrensel küme
A ⊆ E , B ⊆ E ve C ⊆ E olmak üzere
s(A) + s(C') = 16
s(B) + s(C) = 11
s(A') + s(B') = 27
olduğuna göre s(E) kaçtır?
A) 18 B) 19 C) 20 D) 21 E) 22

19. A ve B kümeleri için
s(A \ B) = 7, s(B) = 8
olduğuna göre s(A ∪ B) kaçtır?
A) 7 B) 8 C) 13 D) 15 E) 17

20. A, B ve C kümeleri için
s(A) = 14,
s(B) = 16,
s(C) = 19,
s(A ∩ B) = 9,
s(A ∩ C) = 8,
s(B ∩ C) = 6,
s(A ∩ B ∩ C) = 5
olduğuna göre s(A ∪ B ∪ C) kaçtır?
A) 29 B) 30 C) 31 D) 32 E) 33

21. A \ B kümesinin tümleyeni aşağıdakilerden hangisine eşittir?
A) A' B) B' C) A ∩ B' D) A' ∪ B E) (B \ A)'
Cevap C) A' ∪ B
\ B kümesinin tümleyeni (A \ B)' ifadesini hesaplayalım:
(A \ B)' = A - B' (A'nın B' tümlemesi)
Bu nedenle doğru cevap D) A - B' olacaktır.

22. Yukarıdaki Venn şemasında gösterilen taralı bölgeleri ifade eden küme aşağıdakilerden
hangisidir?
A) (A ∩ B) ∩ C
B) C \ (A ∩ B)
C) (A ∩ C) ∪ (B ∩ C)
D) (A ∪ B) \ C
E) (A ∩ B) \ C
Cevap B) C \ (A ∩ B)

23. A ve B kümelerinin alt küme sayıları toplamı 384’tür. Kümelerin eleman sayıları birer artırılırsa alt küme sayıları toplamı kaç olur?
A) 464 B) 512 C) 604 D) 728 E) 768

24. A ∩ B = {a, b}, A ∩ C = {c, d, e} olduğuna göre A ∩ (B ∪ C) kümesi aşağıdakilerden hangisidir?
A) {a, b, c, d, e} B) {a, b, c, d} C) {a, b} D) {c, d, e} E) {b, c, d, e}
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
= {a,b} ∪ {c,d,e}
= {a,b,c,d,e}
Cevap A) {a, b, c, d, e}

25. [ A ∩ (A ∩ B)' ] ' ∩ (A ∩ B)'
ifadesinin en sade biçimi aşağıdakilerden hangisidir?
A) A B) A' C) B D) B' E) ∅
Cevap B) A'
[ A ∩ (A ∩ B)' ] ' ∩ (A ∩ B)'
[A' ∪ (A ∩ B)] ∩ (A' ∩ B')
[(A' ∪ A) ∩ (A' ∪ B)] ∩ (A' ∪ B')
(A' ∪ A) ∩ (A' ∪ B')
A' ∪ (B ∩ B')
A' ∪ ∅
A'

26. (A ∩ B') ∪ (A ∪ B)' ifadesinin en sade biçimi aşağıdakilerden hangisidir?
A) A' B) A C) B' D) B E) E
Cevap C) B'
(A ∪ B)' = A' ∩ B'
(A ∩ B)' = A' ∪ B'

Şimdi verilen ifadeyi bu kanunlar kullanarak sadeleştirelim:

(A ∩ B') ∪ (A ∪ B)' = (A ∩ B') ∪ [(A') ∩ (B')]
(A ∩ B') ∪ [(A') ∩ (B')] = (A ∩ B') ∪ (A' ∩ B')

Şimdi De Morgan'ın ikinci kanununu kullanarak bu ifadeyi daha da sadeleştirelim:

(A ∩ B') ∪ (A' ∩ B') = (A ∩ B' ∪ A' ∩ B')

Sonuç olarak, verilen ifadenin en sade biçimi A ∩ B' ∪ A' ∩ B' olacaktır.
Doğru cevap C) B'dir.

27. Yukarıda verilen Venn şemasına göre aşağıdaki istenenleri bulunuz.
a) (A ∪ B) \ C b) (A ∪ B) ∪ C c) A' ∪ B'

28. A ve B, E evrensel kümesinin birer alt kümesi olmak üzere
s(A \ B) = 10,
s((A ∪ B)¢) = 7,
s(E) = 25
olduğuna göre s(B) kaçtır?
A) 8 B) 11 C) 15 D) 17 E) 18

29. A, B ve C kümeleri için aşağıda verilen eşitliklerden doğru olanların başına “D”, yanlış
olanların başına “Y” yazınız.
(D) s(A ∪ B) = s(A) + s(B) – s(A ∩ B)
(Y) s(A∪B∪C) = s(A)+s(B)–(A∩ B∩C)
(Y) A x B = B x B
(Y) A x ∅ = A
(D) s(A x B) = s(B x A)
(D) s(A x B) = s(A) · s(B)
(D) s(A ∪ B) = s( A \ B) + s(A ∩ B) + s(B \ A)
(Y) A ∪ B = A ∩ B
(D) A ∪ A¢ = E
(Y) A \ B = A¢ ∪ B
(D) (A ∩ B)¢ = A¢ ∪ B¢
(D) (A¢)¢ = E

30. 70 kişilik bir grupta yalnız İngilizce bilenlerin sayısı yalnız Fransızca bilenlerin sayısının 3
katıdır. Fransızca bilenlerin sayısı 21 ve hiçbir dili bilmeyenlerin sayısı 4 olduğuna göre
İngilizce bilenlerin sayısı kaçtır?
A) 52 B) 51 C) 50 D) 49 E) 48

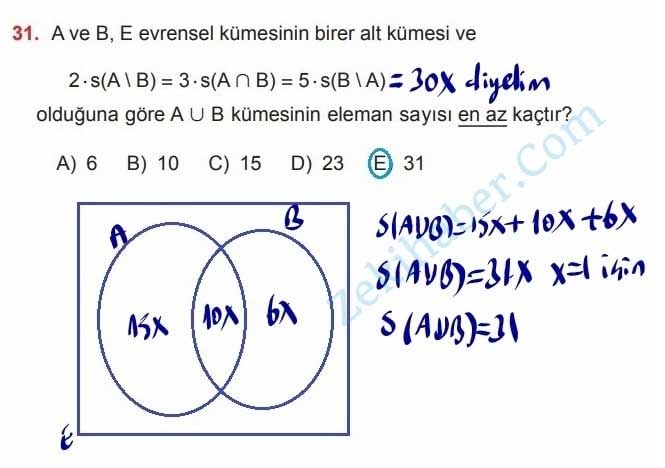
31. A ve B, E evrensel kümesinin birer alt kümesi ve 2 · s(A \ B) = 3 · s(A ∩ B) = 5 · s(B \ A)
olduğuna göre A ∪ B kümesinin eleman sayısı en az kaçtır?
A) 6 B) 10 C) 15 D) 23 E) 31

32. 42 kişilik bir grupta Almanca ve Fransızca bilenler 17 kişi, yalnız Almanca bilenler 9 kişidir.
Bu grupta herkes en az bir dil bildiğine göre yalnız Fransızca bilen kaç kişi vardır?
A) 16 B) 17 C) 18 D) 19 E) 29

33. 40 kişilik bir grupta gözlüklü kızların sayısı, gözlüksüz erkeklerin sayısının 2 katından 1
eksik, gözlüksüz kızların sayısından 1 fazladır.
Gözlüklü erkeklerin sayısı 13 olduğuna göre gruptaki kızların sayısı kaçtır?
A) 24 B) 23 C) 22 D) 21 E) 20

34. s(A) = 5 , s(A x B) = 30 olduğuna göre s(B) kaçtır?
A) 4 B) 5 C) 6 D) 10 E) 15
Cevap C) 6
s(A x B) = s(A) . s(B) = 30
5 . s(B) = 30
s(B) = 30/5 = 6

35. (3x – y, x + 2y) = (7, 7) olduğuna göre x + y toplamı kaçtır?
A) 4 B) 5 C) 6 D) 7 E) 8

36 A = {a, b, c} ve
B = {x | –2 < x < 4, x OE Z }
olduğuna göre s(A x B) kaçtır?
A) 6 B) 9 C) 12 D) 15 E) 16
Cevap D) 15
s(A) = 3
B= {-1,0,1,2,3}
s(B) = 5
s(A . B) = s(A) . s(B) = 3 . 5 = 15

37. A = {1, 5}, B = {2, 6} veriliyor.
Buna göre A x B kümesinin elemanlarını köşe kabul eden dikdörtgenin alanı kaç birimkaredir?
A) 30 B) 16 C) 12 D) 10 E) 6

38. A = {∅, ∪, ∩, ∈} olduğuna göre (s(A))² kaçtır?
A) 9 B) 12 C) 16 D) 20 E) 25
Cevap C) 16
s(A) = 4
s(A)² = 16

Not: Bu sayfadaki bazı soruların cevapları zekihaber.com sitesinden alınmıştır.