10. Sınıf Matematik Ders Kitabı Sayfa 77-78-79-80 Cevapları Miray Yayıncılık

2.1.1 Konu Değerlendirme Soruları

1. A = {1,2, 3} ve B = {4, 5, 6} kümeleri için A’dan B’ye verilen aşağıdaki ilişkilerden hangileri fonksiyondur?

a. f1 = {(1,6), (2, 5), (3, 4)}
b. f2 = {(1> 6), (3, 5), (2, 4), (1,4)}
c. f3 = {(2, 5), (3, 5)}
ç. f4 = {(1,4), (2, 4), (3, 4)}
d. f5 = {(1,5), (2, 4), (3, 4), (1,6), (2, 6)}
Cevap: a ve ç fonksiyondur.

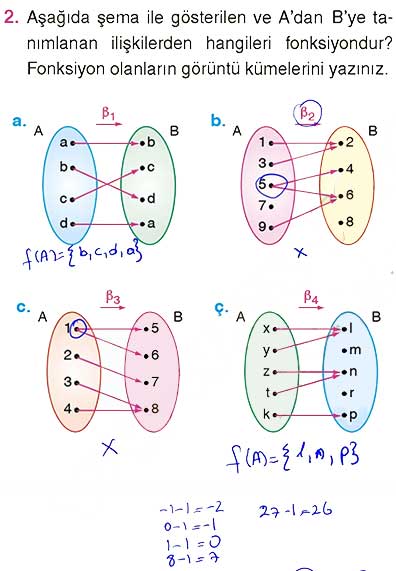
2. Aşağıda şema ile gösterilen ve A’dan B’ye tanımlanan ilişkilerden hangileri fonksiyondur? Fonksiyon olanların görüntü kümelerini yazınız.

a. f(A) = {a, b, c, d}
ç. f(A) = {l, n, p}

3. f:A-B, f(x) = x³ – 1 ve A = {-1, 0, 1, 2, 3} olduğuna göre;

a. f(A) görüntü kümesini bulunuz.
Cevap: a. f(A) = {-2,-1, 0,7,26}

b. f kümesini sıralı İkililer hâlinde yazınız.
Cevap: f = {(-1,-2), (0,-1), (1,0), (2, 7), (3, 26)}

4. f = {(a, 1), (c, 2), (b, 3),(1,2), (3, b)} bir fonksiyon olduğuna göre tanım ve görüntü kümelerini bulunuz.

Tanım Kümesi = {a, b, c, 1,3}
Görüntü Kümesi = {1,2, 3, b}

5. Görüntü kümesi, B = {-2, -1,0,1,2} verildiğine göre aşağıda A → B tanımlanan fonksiyonların tanım kümelerini liste biçiminde yazınız.

a. f(x) =-x + 1 → {-1,0, 1,2, 3 }
b. g(x) = 2x-1 → {-1/2,0, 1/2,1, 3/2}
c. h(x) = x+1/2 → {-5,-3,-1, 1, 3}
ç. k(x) = 1-x/3 → {-5,-2,1,4, 7}
d. m(x) = 2x-1/2 → {-3/2,-1/2,1/2, 3/2, 5/2}
e. n(x) = 1 -3x/2x+3 → {-7,-5/7,-2/5, 1/3, 4}

6. Birçok hastalık durumunda kan nakline ihtiyaç duyulmaktadır. Her kan grubunda, kendi içinde kan alışverişi yapılırken asıl kan grubundan yeterli miktarda kan bulunamaması durumunda farklı kan grupları arasında kan alışverişi yapılabilmektedir. Aşağıdaki tablo kan grupları arasındaki kan alışverişini göstermektedir. Buna göre;

a. K = {0, A, B, AB} olmak üzere tablodaki verileri kullanarak K → K’ye fonksiyon olan ve olmayan birer matematiksel ilişkiyi sıralı İkililerin kümesi şeklinde yazınız.

b Yazdığınız ilişkileri şema ve tablo ile gösteriniz.

7’den 12’ye kadar sorularda aşağıdaki değerlerin her birini bulunuz.

7. f(x) = x + 1
Cevap: -1,2/3, 2, 4

8. f(x) = 1/2x-1
Cevap: 1/5, -3/5, 1,-3

9. f(x) = x2 + 3
Cevap: 7,28/9,4,52

10. f(x) = 2/x²+3
Cevap: 2/7, 9/14, 1/2, 98/151

11. f(x) = √5x + 1
Cevap: Yok, Yok √6 √5√11+1

12. f(x) = Ix — 1I + 3
Cevap: 6, 13/3, 3,6

13’ten 16’ya kadar sorularda aşağıdaki değerlerin her birini bulunuz.

13. g(x) = 2/3x
Cevap: -2/3a, 2a/3, 2/3/a, 2/3a²

14. g(x) = x² + 4
Cevap: a2+ 4, 1/a² + 4, a+ 4, a⁴ + 4

15. g(x) = 1/x²+4
Cevap: 1 /(a² + 4), a2/(4a² + 1), 1/(a + 4), 1 /(a⁴ + 4)

16. g(x) = √2+x²+x⁴
Cevap: √2+a²+a⁴, √2 + 1/a²+1/a⁴, √2+a+a², 2+a⁴+a⁸

17. Aşağıdaki fonksiyonlarda h(a) = 5 koşulunu sağlayan tüm a değerlerini bulunuz.

a. h(x) = 2x + 3 → {1}
b. h(x) = 1/4x+1 → {-1/5}
c. h(x)=√x²16 → {-3, 3}
ç. h(x) = x³ – 3 → {2}
d. h(x) = ³√x+25 → {100}
e. h(x) = |x² – 4| → {-3, 3}

18. Aşağıda kuralı verilen fonksiyonların tanım kümelerini bulunuz.

a. f(x) = 9 – x² → R
b. g(x) = x3 + 3 → R
c. h(x) = √x² → R
ç. k(x)=(√x)² → [0, + ∞)
d. f(x) = √2x+7 → [-7/2,+∞)
e. m(x) = √x+3 → R
f. n(x) = √1 -3x → (-∞,1/3
g. p(x) = 1/(x+2)² → R- {-2}
ğ. r(x) = 4/5-x → R- {5}
h. s(x) = √4/5-x → (-∞,5)
ı. t(x) = 4/5-x → R
i. u(x) = 1/√9-x² → (-3, 3)
j. v(x) = √|x +2|-3 → (-∞.-5] U [1, +oo)
k. z(x) = x+5/| x +2 | —3 → R – {-5, 1}

19. f:R → R ve g:R — R olmak üzere, f(x)= x/2 ve g(x) = -x + 1 veriliyor. f(2a) = g(-2a) eşitliği sağlandığına göre a kaçtır?
Cevap: -1

20. Babası, Hakan’ın yeni kumbarasına 1 TL atmış ve her gün bir önceki gün attığı paradan 2 TL daha fazla para atacağına söz vermiştir. Buna göre;

a. 10. güne kadar her gün Hakan’ın kumbarasında biriken parayı gösteren bir tablo hazırlayınız.

b. Tabloyu inceleyerek geçen gün sayısı (t) ile kumbarada biriken para miktarı (P) arasındaki ilişkiyi analiz ediniz.

c. P’yi, t’nin bir fonksiyonu olarak ifade ediniz.
Cevap: P(t) = t²

21. Bir kenarının uzunluğu x cm ve çevresi 50 cm olan dikdörtgenin alanının; A(x) = x.(25-x) , 0<x<50 fonksiyonu ile verilebileceğini gösteriniz.

22. Üstü açık bir kutu kenar uzunluğu 40 cm olan kare şeklindeki bir kartondan oluşturulacaktır. Öncelikle bu kartonun köşelerinden kenar uzunluğu x cm olan 4 kare kesilip çıkarılıyor. Sonra elde edilen 4 kanat tabanı kare ve yüksekliği x olacak kutunun yanal yüzlerini oluşturmak üzere (noktalı doğrular boyunca) yukarı kaydırılıyor. Buna göre;

a. Kutunun hacmini (V) x’in bir fonksiyonu olarak ifade ediniz.
Cevap: f(x) = (40 – 2x)².x

b. Oluşan kutunun yüksekliği 5 cm ise hacmi kaç cm³ tür? (Bir prizmanın hacminin taban alanı ve yüksekliğinin çarpımı ile bulunduğunu hatırlayınız.)
Cevap: 4500

23. f: M — R, f(x) =’ x2+x , x > 3 ise x2 +2x +1 , x<0 ise 4-3x , 0 < x < 3 ise verildiğine göre f(1) + f(3) değerini bulunuz.
Cevap: 13

24. Levent, Canan’a aklından 1 ile 30 arasında bir sayı tutmasını, bu sayıya 10 eklemesini ve sonucu 2 ile çarpmasını söyler. Daha sonra, sonuçtan 4 çıkarıp kalanı 4’le bölmesini ve sonucu kendisine söylemesini ister.

a. Yukarıdaki durumu modelleyen bir fonksiyon yazınız.
Cevap: f(x) = x/2+4

b. Bu fonksiyonun tanım ve görüntü kümesini yazınız.
Cevap: A = (1, 30), f(A) (9/2, 19)

b. Canan’ın Levent’e söylediği sayı 10 ise Canan’ın aklından tuttuğu sayı kaçtır?
Cevap: 12

25. f; Z ->• Z olmak üzere f(x) = (2m-n)x + m- 2n’dir. f birim fonksiyon ise (m, n) sıralı İkilisini bulunuz.
Cevap: (2/3,1/3)

26. A = {-1, 0,1} ve B = {0, 1, 2} kümeleri veriliyor. f:A — B, f(x) = x-x3 + 1 olduğuna göre f sabit fonksiyon mudur? Neden?
Cevap: f(-1) = f(0) = f(1) olduğundan f sabit fonksiyondur.

27 f: R → R, f(x) = (a – 1 )x² – 3bx- a + b + 3’tür. f sabit fonksiyon olduğuna göre f (45) değeri kaçtır?
Cevap: 2

28. a, b, c E R olmak üzere, f(x) = (a- 1)x + b-4 ve g(x)= 2a-bx/cx+4 veriliyor. f birim fonksiyon ve g sabit fonksiyon ise a+b/c kaçtır?
Cevap: 1

29. Bir ilde uygulanan taksi ücreti tarifesine göre açılış ücreti 2,7 TL olup yolculardan her 1 km için 2,4 TL talep edilmektedir. Buna göre;

a. Taksi ücretini, gidilen toplam yol uzunluğunun (x km) fonksiyonu şeklinde yazınız.
Cevap: f(x) = 2,4x + 2,7

b. Bu ilde taksiye binen bir kişi 24 km’lik bir yol için kaç TL öder?
Cevap: 60,30

c. Bu ilde taksiye binen bir kişi taksi ücreti olarak 74,7 TL ödediğine göre kaç km seyahat etmiştir?
Cevap: 30

30. f: R → R, doğrusal bir fonksiyon ve f (1) = – 3, f(-4) = 2 olduğuna göre f(0) kaçtır?
Cevap: -2

31. A = {0, 1}, B = {-2,-1,0,1,2} kümeleri için f:A^B, f(x) = -x2- 1 ve g:A → B, g(x) = -x – 1 veriliyor. f(A) ve g(A) kümelerini bulunuz, f ve g fonksiyonları eşit fonksiyonlar mıdır? Neden?
Cevap: f(A) = g(A) = {—1, —2}, f(0) = g(0) ve f(1) = g(1) olduğundan f = g dir.

32. f çift fonksiyon olmak üzere aşağıda verilen fonksiyonlardan tek, çift ya da ne tek ne de çift fonksiyon olanları belirleyiniz.

a. y = f(-x) → Çift
b. y = -f(x) → Tek
c. y = f(2x) → Çift
ç. y = f(x/2) → Çift
d. y = f(x)-2 → Çift
e. y = f(x/2+3) → Ne tek ne çift

33. Gerçek sayılar kümesinde tanımlı f ve g fonksiyonları, (f + g)(x) = x² (f-g)(2x) = 2x eşitliklerini sağlıyor. Buna göre f(6)/g(6) ifadesinin eşiti kaçtır?
Cevap: 7/5