ALIŞTIRMALAR
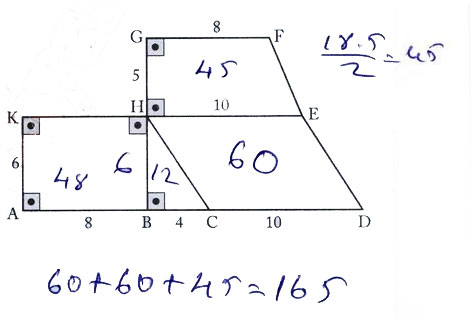
1. Yandaki şekilde ABHK bir dikdörtgen,
HBC bir dik üçgen, CDEH bir paralelkenar,
HEFG ise bir yamuktur.
|AB| = 8 cm,
|BC| = 4 cm,
|KA| = 6 cm,
|CD| = 10 cm,
|GF| = 8 cm,
|HE| = 10 cm ve
|HG| = 5 cm olduğuna göre
ABCDEFGHK bölgesinin alanı kaç cm2 dir?
A) 155 B) 165 C) 175 D) 185
2. Yandaki şekilde verilenlere göre boyalı bölgenin alanını bulunuz.
3. Yandaki eşkenar dörtgen biçimindeki arsanın bir kısmına şekilde gösterildiği gibi yeşil alan, geri kalan yamuk
şeklindeki kısmına ise otel yapılacaktır. Eşkenar dörtgen şeklindeki arsanın bir kenarının uzunluğu 65 metre,
eşkenar dörtgen şeklindeki arsanın karşılıklı kenarları arasındaki dik uzaklık 60 metre olduğuna göre otel için
ayrılmış alan ile yeşil alanın farkını bulunuz
Otel = (65 + 55) . 60 / 2 = 3600 m2
Yeşil alan = 60 . 10 /2 = 300 m2
3600 - 300 = 3300 m2
4. Yandaki şekilde bir tarlaya ait kenar uzunlukları verilmiştir. Tarlanın alanını bulunuz
90 . 135 + (60 + 90) . 60 /2
1215 + 4500
5715 m2
5. Şekilde [FA] ⊥ [AB], [BC] ⊥ [CD]
F, E, D ve A, B, C noktaları kendi aralarında
doğrusaldır.
|DC| = 8 cm,
|AB| = 12 cm,
|FE| = 7 cm,
|BC| = 6 cm
olduğuna göre boyalı bölgenin alanını bulunuz.
(12 + 7) . 8 / 2 + 6 . 8 / 2 = 76 + 24 = 100
6. Alanları eşit olan EFGH ve ABCD dikdörtgenlerinin çevre uzunluklarını karşılaştırınız.
2 . (24 + 5) = 58
2 . (15 . 8) = 46
Ç(EFGH) > Ç(ABCD)
7. Aşağıda bir okula ait plan verilmiştir. Planda yeşil alan paralelkenar, basketbol sahası dikdörtgen,
derslikler yamuk ve süs havuzu eşkenar dörtgen şeklinde gösterilmiştir. Buna göre okulun bahçesindeki
boş kısmın alanı kaç metrekaredir?
A) 10 524 B) 11 216 C) 12 104 D) 12 524
Basket sahası = 18 . 12 = 216
Yeşil alan = 150
Süs havuzu = 10
Derslikler = (60 + 40) . 50 / 2 = 2500
216+ 150 + 10 + 2500 = 2876
140 . 110 = 15400
15400 - 2876 = 12524
8. Kenar uzunlukları cm cinsinden tam sayı olan bir dikdörtgenin alanı 120 cm2 olduğuna göre bu dikdörtgenin
çevre uzunluğu en az kaç cm’dir?
A) 34 B) 44 C) 46 D) 58
a . b = 120
12 . 10 = 120
12 + 12 + 10 + 10 = 44
9. Kenar uzunlukları cm cinsinden tam sayı olan bir dikdörtgenin çevre uzunluğu 60 cm olduğuna göre
bu dikdörtgenin alanının en fazla kaç cm2 olacağını bulunuz.
2(a+b) = 60
a+b = 30
a = 16
b = 14
A = 224m2
10. Çevre uzunlukları eşit olan EFGH ve ABCD dikdörtgenlerinin alanlarını karşılaştırınız.
18 . 4 = 72
15 .7 = 105
A(ABCD) > A(EFGH)
